
Economic assessment
Methods
Two principal methods to analyze the economics of an investment are used in practice: static and dynamic considerations. Static economical analysis compares only yearly averaged savings with the corresponding costs and does not consider the influence of the time of payments in a correct manner. As measures for building or solar systems integrated in buildings show long life times (in the range between 15 years to 25 years and beyond), preferably the methods of dynamic economical analysis should be applied, which fully take into account the importance of time when payments occur.
Static analysis
Nevertheless static analyses are quite commonly used, because they can be carried out with much less mathematical effort than the corresponding dynamic methods. As an example, simple static payback-time analysis (without consideration of interests) compares only initial investments I0 with average annual revenues R due to energy savings in order to get the payback-time n from
 |
(1) |
This (simple) payback-time is just the number of years during which the sum of annual revenues due to energy savings becomes equal to the amount of initial investments. Initial investments are the incremental costs for the solar system and do not involve costs which would arise in any other case for the corresponding building component. Annual revenues are annually avoided, averaged energy costs which consist of annual energy savings multiplied by the costs per energy unit. An initial (incremental) investment of 1.500 EUR, which leads to energy savings of 1.000 kWh with specific costs of 0.06 EUR/kWh, therefore, has a (simple) payback-time of
n = 1,500 EUR / (1,000 kWh/a · 0.06 EUR/kWh) = 25 a (a = years).
This value is situated at the upper bound of the life-time of solar systems. Building measures, however, like choice of thermal insulation or type of glazing implement much larger time spans.
Dynamic analysis
Considering the dynamic nature of capital an initial investment is the origin of a time series of payments which are schematically illustrated in Figure 1. Payments can be negative (expenditures, mainly due to initial investments, interests and costs for maintenance and operation) or positive (revenues, mainly due to saved energy costs). They are subjected to general inflation rates and perhaps different energy inflation rates [1]. For a proper balance of payments the time series of revenues and expenditures has to be discounted on a well defined point of time.
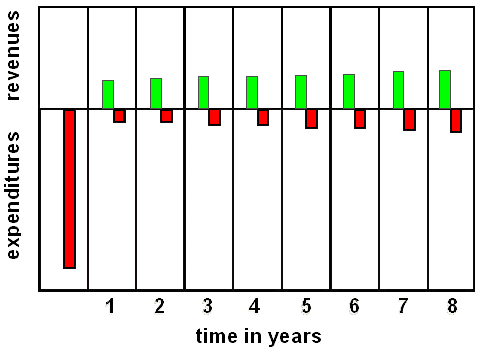 |
| Fig. 1: Time series of payments (revenues and expenditures) as consequence of an initial investment. |
Capital value
The capital value C describes the amount of money which is obtained beyond a fixed (wished or payable) interest rate for capital or a loan. If related to the date of initial investment C becomes
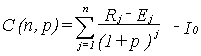 |
(2) |
Equation (2) is valid if the residual (monetary) value of the investment after n years is assumed to be zero. If there are several options of technical systems or alternatives for building, that one with maximum capital value C will be selected. For a given initial investment I0 the capital value C depends very much on the number n of considered years and on the interest rate p.
Revenues Rj in the jth year depend on the solar system performance as well as on the inflation rate e for energy costs. Expenditures Ej in the jth year are costs for operation and maintenance of the solar system or the alternative building solution. These costs are usually assumed to be equal to a fixed percentage f of the initial investment I0 and subjected to the general inflation rate g. With yearly saved energy SE (in kWh) and specific energy costs CE (in EUR/kWh) Rj and Ej become under the assumption of invariable inflation rates e and g
| Rj = SE×CE×(1 + e)j | (3) |
| Ej = f×I0×(1 + g)j | (4) |
In the following, several economic terms to analyze the capital value C are defined and the corresponding formulas are given. The evaluation of a capital value C can be done in different ways. One can calculate the following:
Payback-time
This is defined as that time span n* (in years) since the date of investment during which the initial investment costs I0 including the expected or payable interests (at rate p) have been recovered. C yields:
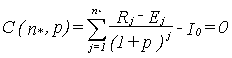 |
(5) |
This is an implicit equation to determine n* as the root of C(n*, p) = 0. In practice, the solution of this equation has to be found by iterative calculations.
The lower the payback-time is, the more economic is the investment. In any case life time of the building measure or a solar system must be longer than its payback-period.
Internal interest rate
This is defined as that interest rate p* (in percent) which makes after a given time period of n years the capital value C equal to zero.
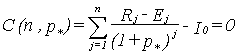 |
(6) |
Again this is an implicit equation to determine p* as a root of C(n, p*) = 0. To solve this equation, iterative numerical algorithms have to be applied.
The internal interest rate p* of a solar or building investment should be as high as possible. In any case the interest rate for capital or loan must be less than the internal interest rate p*.
Annuity
This is defined as a constant amount A payable at the end of every n interest periods (years) for which the sum of payments is equal to the future amount of the initial capital value C after
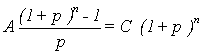 |
these n years:
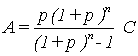 |
(7) |
Inserting C from equation (2) results in an explicit expression for the annuity A. The greater the annuity is, the better is the (building/solar) investment. In no case is annuity A allowed to be negative (equivalent to C < 0).
The annuity factor A/C is given by:
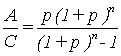 |
(8) |
an this depends merely on interest rate p and number of interest periods n. It is that equal fraction of the initial amount C which has to be paid at the end of each interest period in order to pay off the future amount of the capital value C (the accumulated gains or debts) after n years.
For the special case where revenues minus expenditures is constant for every year, the annuity can easily be calculated from equations (7) and (2) and yields:
 |
(9) |
In other words, the total annuity A is the difference between the surplus of revenues over expenditures (R - E) on the one hand and the annuity A(I0) for the initial investment I0 on the other hand.
For the users of the IDEA-software exists a special tool (Economic Evaluation) which calculates all interesting values for an economic evaluation of a solar- or building-related energy saving system (payback-time, internal interest rate, annuity, required initial funding, required energy price, required energy price increase) under a user-friendly surface.
References:
[1] K.W. Boer: Payback of solar systems. Solar Energy, vol. 20 (1978), pp. 225-232.
[2] G.T. Stevens: Economical and financial
analysis of capital investments. John Wiley & Sons, New York, Chichester,
Brisbane, Toronto, 1979.